Looney Tunes/Kladblok: verschil tussen versies
| Regel 26: | Regel 26: | ||
| Capaciteit || C || farad || F || [[Condensator]] | | Capaciteit || C || farad || F || [[Condensator]] | ||
|- | |- | ||
| − | | Zelfinductie || L || henry || H || [[Spoel]] | + | | Zelfinductie || L || henry || H || [[Spoel]] |
|- | |- | ||
|} | |} | ||
| Regel 67: | Regel 67: | ||
'''Praktijkvoorbeeld:'''<br/> | '''Praktijkvoorbeeld:'''<br/> | ||
Een motor in een locomotief heeft een weerstand. Zet je spanning op de baan, dan zal er een stroom door de motor gaan lopen. Zet je twee locomotieven op de baan, dan loopt er twee keer zoveel stroom. Sluit je ook lampjes aan, dan zal ook daar een stroom doorheen gaan lopen. Een trafo moet dus stroom leveren aan alle in werking zijnde verbruikers. Je kunt een beperkt aantal verbruikers aansluiten omdat de stroom uit de trafo niet onbeperkt is. <br/> | Een motor in een locomotief heeft een weerstand. Zet je spanning op de baan, dan zal er een stroom door de motor gaan lopen. Zet je twee locomotieven op de baan, dan loopt er twee keer zoveel stroom. Sluit je ook lampjes aan, dan zal ook daar een stroom doorheen gaan lopen. Een trafo moet dus stroom leveren aan alle in werking zijnde verbruikers. Je kunt een beperkt aantal verbruikers aansluiten omdat de stroom uit de trafo niet onbeperkt is. <br/> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Met de wet van Ohm kunnen we spanning, stroom en weerstand berekenen. Elke weerstand gedraagt zich volgens de wet van Ohm. Dus ook in een grote schakeling met veel weerstanden is de wet van Ohm geldig voor de hele schakeling maar ook voor elk deel van de schakeling. | Met de wet van Ohm kunnen we spanning, stroom en weerstand berekenen. Elke weerstand gedraagt zich volgens de wet van Ohm. Dus ook in een grote schakeling met veel weerstanden is de wet van Ohm geldig voor de hele schakeling maar ook voor elk deel van de schakeling. | ||
Versie van 11 aug 2016 13:46
De basis
Om te zorgen dat verdere begrippen duidelijk zullen zijn staan hieronder eerst de elektrische grootheden, met hun naam, eenheid en een artikel waarin dit verder uitgelegd wordt.
| Tabel grootheden | ||||
|---|---|---|---|---|
| Grootheid | Afkorting | Eenheid | Afkorting | zie ook artikel |
| Elektrische lading | Q | coulomb | C | - |
| Spanning | U | volt | V (=J/C) | Dit artikel |
| Stroomsterkte | I | ampère | A (=C/s) | Dit artikel |
| Weerstand | R | ohm | Ω | Weerstand |
| Vermogen | P | watt | W (=J/s) | Vermogen, arbeid en rendement |
| Arbeid | W | joule of wattseconde | J | Vermogen, arbeid en rendement |
| Capaciteit | C | farad | F | Condensator |
| Zelfinductie | L | henry | H | Spoel |
De begrippen stroom, spanning en weerstand
Veel modelspoorders hebben geen technische achtergrond en daarom kan het nog wel eens verwarrend zijn als er gesproken wordt over spanning en stroom. Dit komt omdat er vaak gedacht wordt dat hiermee hetzelfde bedoeld wordt, terwijl het twee hele verschillende begrippen zijn. Het zijn echter zeer belangrijke begrippen om te snappen wat de basis principes van de elektrische modeltrein zijn.
Om te beginnen worden hieronder eerst kort de begrippen uitgelegd, om hierna het verband tussen deze uit te leggen.
Stroom
Elektrische stroom duidt de de mate van verandering van de elektrische lading in de tijd uit, en wordt gemeten in ampère (A). Dus hoeveel elektronen er eigenlijk elke seconde door een draad/component heen bewegen. Omdat het gaat over een beweging van elektronen valt dus te zeggen dat stroom loopt.
Spanning
Elektrische spanning is een potentiaalverschil tussen twee punten, gemeten in volt (V). De spanning geeft aan hoeveel energie het voor de elektronen kost om van het ene punt naar het andere punt te bewegen. Omdat dit gemeten wordt over twee punten valt te zeggen dat spanning staat.
De verwarring tussen stroom en spanning
Er staat dus geen 'stroom op een stopcontact'. Er staat alleen spanning op, die ervoor zorgt dat er een stroom kan gaan lopen als er een apparaat aangesloten wordt. Of even stroom op de modelbaan zetten daar geldt hetzelfde voor, er staat alleen spanning op de baan, welke ervoor zorgt dat er een stroom gaat lopen.
Weerstand
Voorbeeld:
Stel, je vult een emmer met water en zet die op een verhoging. In de bodem van de emmer zit een gaatje met een slang waarin een kraan zit gemonteerd. Als de kraan dicht zit, zal er geen water uit de emmer stromen. Draai je de kraan open, dan zal er een dikkere straal water uit de slang lopen, naarmate de kraan verder opengedraaid wordt. Het water wil van hoog naar laag stromen.
Toepassing:
In het voorbeeld staat het water stil, zolang de kraan dicht zit. Toch drukt het water tegen de kraan. Er is geen waterstroom. Vergelijk het water met elektriciteit en de kraan kun je met een schakelaar vergelijken. Er staat wel elektrische spanning, maar er loopt geen elektrische stroom als de schakelaar open staat. Zet je de schakelaar om, dan begint meteen de stroom te vloeien. De stroom vloeit van plus naar min. De schakelaar is niet regelbaar zoals een kraan, maar een weerstand kan wel regelbaar zijn, dus we kunnen de kraan ook vergelijken met een regelbare weerstand. Verhoog je de weerstand, dan gaat er minder elektrische stroom lopen.
Wet van Ohm
Elektriciteit kun je niet zien. Daarom wordt er veel van berekeningen gebruik gemaakt, om bijvoorbeeld te weten hoeveel stroom ergens doorheen gaat. Een belangrijke formule daarbij is de wet van Ohm. Die zegt: weerstand is de verhouding tussen spanning en stroom. Dus je kunt de weerstand van wat draadjes en schakelaars en lampjes en dergelijke berekenen, als je de spanning en de stroom weet. Weet je de weerstand en de spanning, dan kun je berekenen hoeveel stroom door het geheel loopt.
Symbolen:
In formules gebruikt men het liefst symbolen, in plaats van de volledig naam.
- Stroom geeft men aan met I, de eenheid is ampère (A). Voorbeeld: I = 0,13 A
- Spanning geeft men aan met U, de eenheid is volt (V). Voorbeeld: U = 16 V
- Weerstand geeft men aan met R, de eenheid is ohm (Ω). Voorbeeld: R = 123 Ω
Praktijkvoorbeeld:
Een motor in een locomotief heeft een weerstand. Zet je spanning op de baan, dan zal er een stroom door de motor gaan lopen. Zet je twee locomotieven op de baan, dan loopt er twee keer zoveel stroom. Sluit je ook lampjes aan, dan zal ook daar een stroom doorheen gaan lopen. Een trafo moet dus stroom leveren aan alle in werking zijnde verbruikers. Je kunt een beperkt aantal verbruikers aansluiten omdat de stroom uit de trafo niet onbeperkt is.
Met de wet van Ohm kunnen we spanning, stroom en weerstand berekenen. Elke weerstand gedraagt zich volgens de wet van Ohm. Dus ook in een grote schakeling met veel weerstanden is de wet van Ohm geldig voor de hele schakeling maar ook voor elk deel van de schakeling.
Formule:
R = U / I Hierbij is :
- R de weerstand in ohm (Ω)
- U is de spanning in volt (V)
- I is de stroom in ampère (A)
Afgeleide formules:
- U = I * R
- I = U / R
Voorbeeld 1
Een gloeilampje is aangesloten op een batterij van 9V. Er vloeit een stroom door van 0.5A. Hoe groot is de weerstand van het gloeilampje? Volgens de wet van Ohm is R = U / I. hieruit volgt dat R = 9V / 0.5A. Als we dit uitrekenen krijgen wet het volgende: R = 18Ω.
Voorbeeld 2
Over een weerstand van 100Ω staat een spanning van 4.8V(bv. 4 herlaadbare baterijen). Welke stroom vloeit er door de weerstand?
Uit R = U / I kunnen we de formule I = U / R afleiden. In dit geval is I = 4.8V / 100Ω. We rekenen uit: I = 0.048A = 48mA.
Voorschakel weerstand berekenen:
Sommige componenten hebben een maximum spanning. om te voorkomen dat deze overschreden wordt, kun je een voorschakel weerstand gebruiken. De waarde berekenen gebeurd m.b.v. de wet van Ohm. stel: we hebben een voeding die 24V gelijkspanning levert. Op het lampje dat we willen gebruiken staat het volgende: 0.5A 16V We hebben dus een voorschakel weerstand nodig waarover 8V valt.(24V - 16V = 8V) We hebben nu de spanning over (8V) en de stroom(0.5A) door de weerstand.
Volgens de wet van Ohm is R = U / I dus R = 8V / 0.5A = 16Ω. Deze weerstand is beschikbaar, dus hoeven we niet af te ronden. Let ook op het vermogen dat de weerstand wegstookt, deze is gedefinieerd als P = U * I. En dus verstookt de weerstand P = 8V * 0.5A = 4W. Om te zorgen dat de weerstand dit veilig kan verstoken kunt u het beste een 5W weerstand gebruiken. Meer info is op de Vermogen, arbeid en rendement pagina te vinden.
Fouten vinden
Rekenfouten kan iedereen maken. Als je elektronica maakt voor je baan, die je duizenden euro's heeft gekost, wil je natuurlijk niet dat je baan beschadigd raakt door een rekenfout. De volgende dingen kunnen helpen bij de controle:
- Bekijk je uitkomst. Een spanning van 100kV (kilovolt = 1000V) is niet echt realistisch.
- Opnieuw intikken in je rekenmachine, en kijken of je hetzelfde resultaat hebt.
- De wet van Ohm kun je omvormen. maak hiervan gebruik: Laten we eens voorbeeld 1 controleren: R = U / I dus U = I x R. bij voorbeeld 1 moet dus het volgende gelden: 9V = 0.5A x 18Ω. Dit klopt, de berekening was dus juist.
Serie en parallel
Serie
Definitie
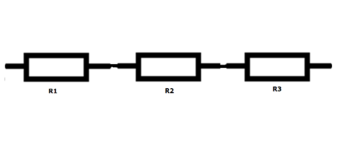
2 of meer verbruikers zijn in serie geschakeld, wanneer het eindpunt van de 1e verbruiker verbonden is met het beginpunt van de 2e verbruiker, het eindpunt van de 2e verbruiker verbonden is met het beginpunt van de 3e verbruiker.
Algemeen
Wanneer we verbruikers in serie schakelen, zal de stroom door deze gelijk zijn, de spanningen zullen verschillen (recht evenredig met de weerstandswaarde).
Formules
Bij een serieschakeling geldt:
- Itotaal = I1 = I2 = I3 = …
- Utotaal = U1 + U2 + U3 + …
- Rtotaal = R1 + R2 + R3 + …
Voorbeeld 1
2 weerstanden zijn in serie geschakeld. Over de ene weerstand staat 1V, over de andere 2V. De totale spanning is 3V. De ene weerstand verstookt dus 1/3 van de totale spanning, de andere 2/3. De stroom door de weerstanden is wel gelijk.
Stel dat de eerste weerstand 100Ω bedraagt, hoeveel ohm is de tweede weerstand dan?
de spanningen verhouden zich als 1 en 2, en de stroom is gelijk, dus de weerstanden hebben dezelfde verhouding: de 2e weerstand is 200Ω.
Voorbeeld 2
Een weerstand van 100Ω is in serie geschakeld met een weerstand van 900Ω. Over de eerste weerstand staat een spanning van 1V.
Hoeveel spanning staat er over de 2e weerstand?
De 2e weerstand is 9 keer zo groot, en de stroom is gelijk, dus heeft de spanning dezelfde verhouding: de spanning over de 2e weerstand is dan 9V.
Parallel
Definitie
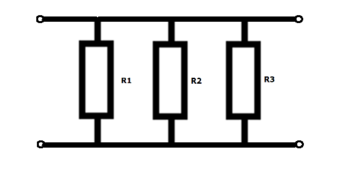
2 of meer verbruikers zijn parallel geschakeld, wanneer de beginpunten enerzijds en de eindpunten anderzijds met elkaar zijn verbonden.
Algemeen
Wanneer we verbruikers in parallel schakelen, zal de spanning gelijk zijn, de stromen zullen verschillen (recht evenredig met de weerstandswaarde).
Formules
Bij een serieschakeling geldt:
- Itotaal = I1 + I2 + I3 +…
- Utotaal = U1 = U2 = U3 =…
- Rtotaal = 1 / ((1/R1) + (1/R2) + (1/R3) + …)
Gemengde schakeling
Een gemengde schakeling is een schakeling waarbij er een combinatie van serie en parallel gebruikt wordt. Dit soort schakelingen kunnen ook met de Wet van Ohm doorgerekend worden, als is het vaak lastiger om te doen.